Partial Least Squares-Correspondence Analysis (PLS-CA): A New Method to Analyze Common Patterns in Measures of Cognition and Genetics

With the introduction of large scale studies (such as the Alzheimer's Disease Neuroimaging Initiative; ADNI) researchers in  neuroscience, and genetics are now routinely collecting, and sharing, a wide variety of very large data sets (e.g., neuroimaging, genomes, cognitive measures) whose analysis requires suitable statistical methods. In general, the structure and variety of these data sets preclude the use of standard hypothesis driven or multivariate techniques (such as multiple regression or discriminant analysis).
 
Interestingly, most of the data in genetics-based cognition research---such as questionnaires and single nucleotide polymorphisms (SNPs)---are nominal variables and structured in blocks or tables (e.g., memory tasks for behavior; chromosomes for a genome). Nominal variables can be analyzed with multivariate techniques such as Correspondence Analysis (CA) and Discriminant Correspondence Analysis (DiCA). CA-based methods are to qualitative data what principal components-based methods are to quantitative data.
 
However, CA and DiCA are suitable to analyze one data set. In order to reveal common information between two data sets (e.g., cognitive measures and genetics) we adapted the well-known Partial Least Squares Correlation (PLSC) method (suitable for quantitative measurements) so that it can be used with nominal data. This new approach, called PLS-CA, integrates in a common framework PLSC and CA. PLS-CA reveals patterns of co-occurrence of SNPs and behavioral measures --- or connectivity between genetics and behavior. Furthermore, we extend the PLS-CA framework to predict group membership (e.g., clinical group). This new technique, called Discriminant PLS-CA reveals factors common to two nominal data tables, while accounting for a priori discriminant information for observations. Discriminant PLS-CA relates causal data (i.e., clinical groups), to relational data (i.e., genetics and cognition), similar to Multi-block PLSC.
 
PLS-CA and Discriminant PLS-CA include inferential non-parametric cross validation techniques such as permutation tests, jackknifing, and bootstrapping.
 
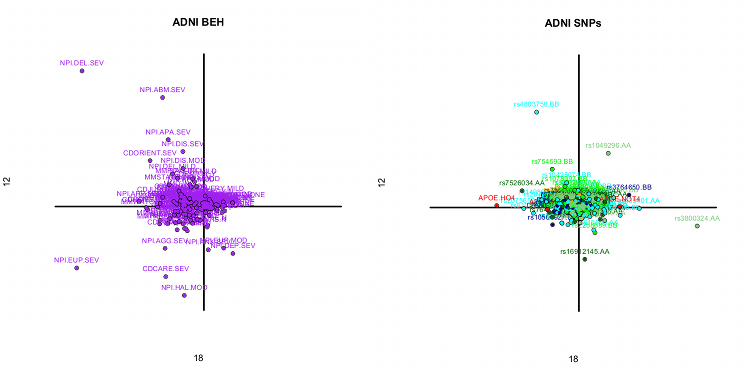
We illustrate the PLS-CA framework (and its discriminant extension) with data from the ADNI clinical and genetic datasets. Our goal is to relate genomic (SNPs) and behavioral data. Results show patterns of genetic variations associated to both healthy and dysfunctional cognitive traits, as well as genetic variations for clinical groups.